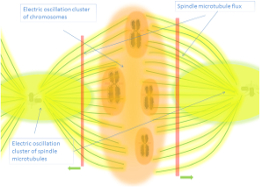
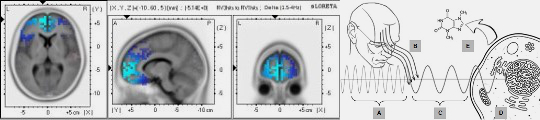
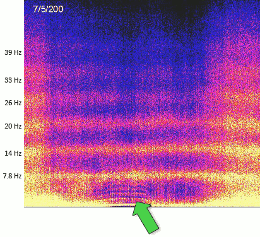
Electromagnetism & Fröhlich Modes
Collective large-scale vibrational modes involving microwave absorption and emission

Fröhlich modes represent collective electromagnetic (EM) excitations within biological systems, driven by dipolar interactions and out-of-equilibrium dynamics. This section explores the foundational principles of Fröhlich condensation and its relevance to cellular coherence, biomolecular interactions, and long-range communication. ...

This section synthesizes findings on the experimental validation of Fröhlich condensation, the influence of terahertz radiation on protein structures, and the implications of these phenomena for understanding biological coherence. The evidence underscores the importance of endogenous electromagnetic fields in orchestrating cellular processes and suggests a foundational role in biological regulation and information processing.

The concept of Fröhlich modes, first proposed in the 1960s, describes a state of coherence in biological systems far from thermal equilibrium. This theoretical framework suggests that collective oscillations in biological macromolecules, driven by metabolic energy, could lead to Bose-Einstein-like condensation in biological systems. Recent experimental studies have provided evidence supporting this hypothesis, linking Fröhlich modes to electromagnetic fields, cellular communication, and long-range coherence. This section explores these findings, emphasizing their implications for biological information processing and systemic organization.

Key Findings and Experimental Evidence:

• Terahertz Radiation and Structural Changes in Proteins:

  • Studies on bovine trypsin crystals irradiated with 0.5 THz radiation demonstrate increased anisotropy in atomic displacements, indicating the presence of delocalized vibrational modes (Ahlberg Gagnér et al., 2019).

  • These modes, consistent with Fröhlich’s predictions, suggest a mechanism for protein-protein interactions and biochemical regulation at terahertz frequencies.

• Quantum Fluctuations in Fröhlich Condensates:

  • Research on molecular vibrations driven far from equilibrium has identified quantum fluctuations in Fröhlich condensates. These findings highlight the potential for coherent oscillatory states to mediate long-range biological interactions (Zhang et al., 2018).

• Out-of-Thermal Equilibrium Oscillations:

  • Experimental models using bovine serum albumin (BSA) reveal absorption features around 0.314 THz when driven into non-equilibrium states. These observations provide direct evidence for the existence of Fröhlich modes in living systems (Nardecchia et al., 2017).

Mechanisms and Implications:

• Energy Localization and Long-Range Coherence:

  • Fröhlich modes enable the localization of vibrational energy, creating coherent states that facilitate efficient energy transfer and information processing within cells.

  • These mechanisms align with the observation of collective vibrational modes in protein structures, contributing to intracellular coordination.

• Interaction with Endogenous Electromagnetic Fields:

  • Fröhlich modes interact with endogenous EM fields generated by metabolic activity, influencing cellular communication and systemic regulation.

  • The periodic transformations between phonons and photons in Fröhlich condensates suggest a dynamic interplay between mechanical and electromagnetic energies.

• Biological Implications:

  • Fröhlich modes have been implicated in various biological phenomena, including protein folding, enzymatic reactions, and signal transduction.

  • Their role in coordinating long-range interactions highlights their importance in maintaining biological coherence and systemic organization.

Future Directions and Applications:

• Terahertz Spectroscopy in Biomedical Research:

  • Advances in terahertz spectroscopy offer new tools for investigating Fröhlich modes and their role in health and disease.

  • Potential applications include disease diagnosis, understanding protein misfolding disorders, and developing terahertz-based therapeutic interventions.

• Quantum and Biophysical Studies:

  • Further research on the quantum properties of Fröhlich modes could elucidate their role in information processing and coherence in biological systems.

Conclusion: The experimental validation of Fröhlich modes underscores their significance in biological systems. By facilitating long-range coherence and efficient energy transfer, these modes contribute to the regulation and organization of cellular processes. Their interaction with endogenous electromagnetic fields offers a compelling framework for understanding biological coherence and opens avenues for novel biomedical applications.

Keywords: Fröhlich modes, electromagnetic fields, terahertz radiation, biological coherence, protein dynamics, quantum fluctuations.

Very related sections:

Endogenous Fields & Mind
EM & Fröhlich Modes